报告人：杨卫华 教授 太原理工大学

报告题目：On the toughness of a graph

时间：2025年3月26日14:30-16:00

地点：数学楼2-3会议室

摘要：

      Let 0 be a real number. The graph 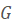 is said to be -tough if for every cutset  of 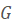 the ratio of to the number of components of 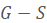 is at least . Chvàtal conjectured that there exists a positive real number 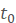 such that every 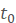-tough graph is Hamiltonian. This conjecture holds for planar graphs with toughness greater than  by the classic result of Tutte that every 4-connected planar graph is Hamiltonian. In 1999, Owens constructed a class of maximal planar graphs with toughness arbitrarily close to , which contain no 2-factors. He then posed the question of whether there exists a maximal planar graph with toughness exactly  and with no 2-factor. This question was recently answered affirmatively by Shan. This naturally leads to the question: under what conditions does a -tough maximal planar graph contain a 2-factor? In this talk, we provide a sufficient condition for the existence of 2-factors in -tough maximal planar graphs, stated as a bound on the distance between vertices of degree 3. In addition, we also confirm Chvàtal’s conjecture for the class of 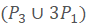-free graphs. Furthermore, we have also studied a class of spanning graphs of -tough graphs. 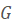A graph  is minimally -tough if the toughness of 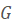 is  and the deletion of any edge from decreases the toughness of 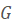. Katona et al. conjectured that every minimally -tough graph has a vertex of degree 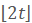. For this conjecture, we have investigated three classes of graphs: triangle-free graphs, claw-free graphs and 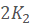-free graphs.

报告人简介：

     杨卫华，太原理工大学数学学院教授、博士生导师，数学学院院长。主要研究方向为图论与人工智能，在JGT、SIAM DM、DM等发表SCI论文100余篇；主持国家自然科学基金4项。现任中国运筹学会理事、图论组合分会理事副秘书长；中国工业与应用数学学会理事、图论组合及应用专业委员会常务理事；山西省工业与应用数学学会副理事长等职。

邀请人：王 卫 教授